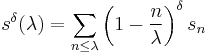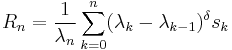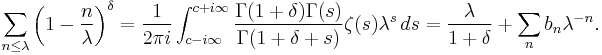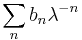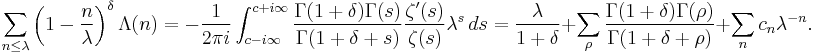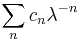Riesz mean

In mathematics, the Riesz mean is a certain mean of the terms in a series. They were introduced by Marcel Riesz in 1911 as an improvement over the Cesàro mean[1][2]. The Riesz mean should not be confused with the Bochner–Riesz mean or the Strong–Riesz mean.

Contents

Definition

Given a series 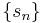\{s_n\}, the Riesz mean of the series is defined by

s^\delta(\lambda) = \sum_{n\le \lambda} \left(1-\frac{n}{\lambda}\right)^\delta s_n

Sometimes, a generalized Riesz mean is defined as

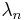R_n = \frac{1}{\lambda_n} \sum_{k=0}^n (\lambda_k-\lambda_{k-1})^\delta s_k

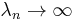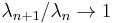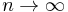Here, the \lambda_n are sequence with \lambda_n\to\infty and with \lambda_{n%2B1}/\lambda_n\to 1 as n\to\infty. Other than this, the 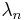\lambda_n are otherwise taken as arbitrary.

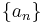Riesz means are often used to explore the summability of sequences; typical summability theorems discuss the case of s_n = \sum_{k=0}^n a_n for some sequence \{a_n\}. Typically, a sequence is summable when the limit 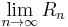\lim_{n\to\infty} R_n exists, or the limit 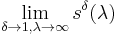\lim_{\delta\to 1,\lambda\to\infty}s^\delta(\lambda) exists, although the precise summability theorems in question often impose additional conditions.

Special cases

Let 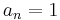a_n=1 for all n. Then

\sum_{n\le \lambda} \left(1-\frac{n}{\lambda}\right)^\delta = \frac{1}{2\pi i} \int_{c-i\infty}^{c%2Bi\infty} \frac{\Gamma(1%2B\delta)\Gamma(s)}{\Gamma(1%2B\delta%2Bs)} \zeta(s) \lambda^s \, ds = \frac{\lambda}{1%2B\delta} %2B \sum_n b_n \lambda^{-n}.

Here, one must take 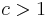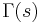c>1; \Gamma(s) is the Gamma function and 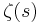\zeta(s) is the Riemann zeta function. The power series

\sum_n b_n \lambda^{-n}

can be shown to be convergent for 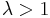\lambda > 1. Note that the integral is of the form of an inverse Mellin transform.

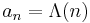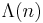Another interesting case connected with number theory arises by taking a_n=\Lambda(n) where \Lambda(n) is the Von Mangoldt function. Then

\sum_{n\le \lambda} \left(1-\frac{n}{\lambda}\right)^\delta \Lambda(n) = - \frac{1}{2\pi i} \int_{c-i\infty}^{c%2Bi\infty} \frac{\Gamma(1%2B\delta)\Gamma(s)}{\Gamma(1%2B\delta%2Bs)} \frac{\zeta^\prime(s)}{\zeta(s)} \lambda^s \, ds = \frac{\lambda}{1%2B\delta} %2B \sum_\rho \frac {\Gamma(1%2B\delta)\Gamma(\rho)}{\Gamma(1%2B\delta%2B\rho)} %2B\sum_n c_n \lambda^{-n}.

Again, one must take c > 1. The sum over ρ is the sum over the zeroes of the Riemann zeta function, and

\sum_n c_n \lambda^{-n} \,

is convergent for λ > 1.

The integrals that occur here are similar to the Nörlund–Rice integral; very roughly, they can be connected to that integral via Perron's formula.

See also

References